Introduction to the Mill CPU Programming Model

Author
Posts
Will_Edwards
Moderator
February 7, 2014 at 10:54 am
Post count: 98
#599 |
The Mill is a new CPU architecture designed for very high single-thread performance within a very small power envelope.
The Mill has a 10x single-thread power/performance gain over conventional out-of-order (OoO) superscalar architectures, yet runs the same programs without rewrite.
The Mill is an extremely-wide-issue, statically scheduled design with exposed pipeline. High-end Mills can decode, issue, and execute over thirty MIMD operations per cycle, each cycle.
The Mill architecture is able to pipeline and vectorise almost all loops, including while loops and loops containing calls and flow control.
The pipeline is very short, with a mispredict penalty of just five cycles.
Processor Models
The Mill is a family of processor models. Models differ in various parameters that specify their performance and power constraints, such as the width of their vector units, the functional units, number of pipelines and belt length.
All Mills can run the same code, however. Code is compiled to an intermediate representation for distribution, and specialisation for a particular Mill processor model is done by a specialising compiler at software installation time or on-demand as needed.
The Belt
The Mill is a belt machine. There are no general-purpose registers.
Functional units (FUs) can read operands from any belt position. All results are placed on the front of the belt.
The belt is a fixed size, and the exact size is dependent on the precise Mill model. When values are inserted at the front of the belt, a corresponding number of old values are pushed off the back end of the belt.
The items on the belt are referenced temporally, by their position relative to the front of the belt, which changes as the belt advances. The belt advances some number of items after each cycle, depending upon how many values were returned by ops finishing that cycle.
For example, add is issued with the operands 2 and 5. This scalar add takes one cycle, so before the next cycle the sum of these two values is inserted at the front of the belt, pushing the oldest item off the back end of the belt.
[See talk: The Belt]
Exposed Pipeline
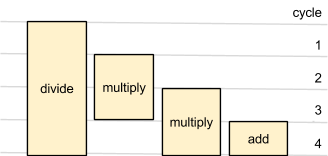
The number of cycles each operation takes is fixed, and known to the compiler. There are no variable-latency instructions other than load.
A pipeline can be told to do one operation each cycle. These operations take some number of cycles, e.g. an add may take one cycle but a multiplication takes 3 cycles.
Even if the pipeline is part-way through an operation, you can still instruct it to start further operations on subsequent cycles, and it will perform these operations in parallel.
For example, a 3-cycle multiplication is started. In the next cycle, a 1-cycle addition is started. The addition inserts its result at the front of the belt at the end of the cycle, while the multiplication is still ongoing. On the next cycle, the result of the addition is on the belt – and can be used as an input to other operations. The multiplication is nearing completion but the pipeline is ready to start another operation.
If two operations in the pipeline finish on the same cycle, they are inserted onto the belt in FIFO order; the operation that was started first is inserted first.
There are very few examples of hazards between operations, and they are CPU -model specific. It may be that two particular operations cannot execute in parallel inside the pipeline, and if this happens the CPU will detect it and fault. But the compiler knows about these exceptions, and does not try and schedule them.
An operation can return more than one result. For example, an integer divide operation may return both the quotient and the remainder, as two separate values. Furthermore, calls (detailed below) can return more than one value too.
Items that fall off the end of the belt are lost forever. Best belt usage results from producers producing as close to their consumers as possible. Belt items requiring an extended lifetime can be saved in Scratch, detailed below.
[See talk: The Belt]
Scalars and Vectors
All Mill arithmetic and logic operations support vectors. Mill operations are SIMD, and scalar values are vectors of length 1.
Each belt item is tagged with its element width and its scalarity (single or full vector of elements). Elements may be 1, 2, 4, 8 or 16 bytes. The vector length is also a fixed length in bytes and is Mill -model -specific.
If a particular Mill -model does not support any particular widths, these are emulated in software transparently by the compiler.
Vector elements can be marked as missing using a special None metadata marker (detailed below). This allows operations on partial vectors.
Operations support all meaningful combinations of operand scalarity. You can add an single integer to every element in a larger vector, for example, or perform a comparison between two vectors.
The Mill has narrow and widen operations, which increase and decrease the width of each element in the operand respectively. Narrow produces a vector of half-width elements and widen produces two vectors of double-width elements.
The Mill also has widen-versions of add and multiply operations, which return vectors of elements double the width of their widest operands, and therefore cannot overflow.
There is an extract operation for extracting elements from vectors to make scalar belt items, and a shuffle operation for rearranging (or duplicating) the elements within a belt item.
The meta-data does not encode the data types. Code can interpret an element as a pointer, float, fraction, signed integer or unsigned integer. There are separate operations for pointers, floating point, fractions, signed integers and unsigned integers. The compiler knows the type of the operands, and encodes this in the operations it issues.
Operations may have different latencies for different element widths. The compiler knows the size and width of all items on the belt at all times, so it knows the latencies. The operations themselves do not encode the operand sizes and the latencies for most sizes are consistent so the compiler can often share code for templated functions which operate on different sized primitives and reuse a single shared function.
[See talk: Metadata]
Instructions and Pipelines
The functional units in a pipeline can, collectively, issue one operation per cycle. But the Mill has lots of pipelines, and each pipeline can issue an operation each cycle, sustained.
The Mill CPU is a VLIW (Very Long Instruction Word) machine. The operations that issue each cycle are collectively termed the instruction.
Different pipelines have different mixes of FUs available, and the number of pipelines and their FU mix is Mill -model specific. There may be 4 or 8 integer pipelines and 2 or 4 floating point pipelines, for example. There are pipelines that handle flow control and pipelines that handle load and saves. In a high-end Mill “Gold” CPU there are 33 pipelines, so the Mill Gold CPU can issue 33 operations per cycle, sustained:
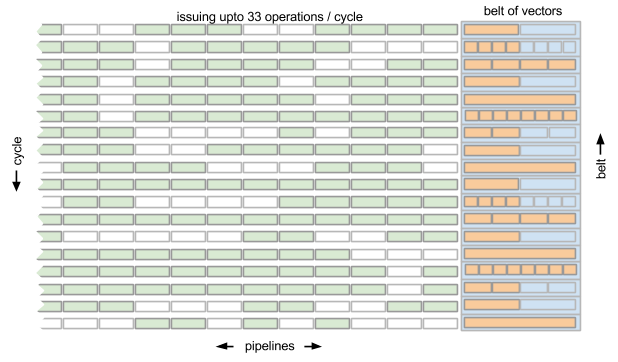
The pipelines in the Mill Gold CPU are:
- 8 pipes that do single output “reader” operations
- 4 pipes that can do either integer (including multiply) or binary floating point (also including multiply) operations
- 4 pipes that can only do integer (not including multiply) operations
- 4 pipes that can do either immediate constant, load/store or control transfer (branch, call) operations
- 4 pipes that can do either immediate constant or load/store operations
- 4 pipes that can do pick operations
- 5 pipes that can do “writer” operations
Width, Length and Height
The key parameters that define the Mill CPU are called its Width, Length and Height:
- Width is the number of pipelines
- Length is the number of belt items
- Height is the number of elements in a vector
These parameters vary between models.
Phasing
Like most microprocessors, the Mill has a multi-stage pipeline.
The Mill has fewer stages than conventional architectures such as classic RISC or modern OoO processors which typically have 10-14 stages (the Intel Pentium 4 peaked with 31 stages).
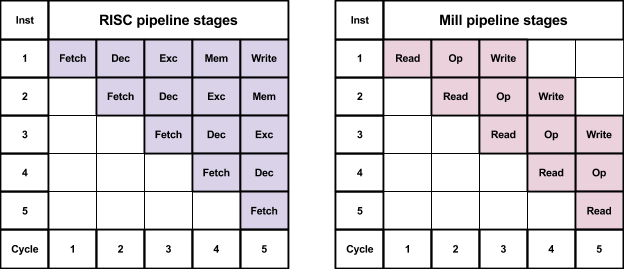
On a conventional microprocessor, each instruction passes through several stages. The individual operations in the instruction pass through the same stages at the same time.
However, the Mill issues the individual operations in an instruction in specific phases and Mill phases in an instruction are issued across several cycles.
There are five phases in the Mill instruction:
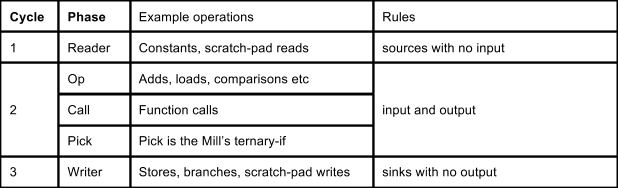
Decode happens during the first cycle and the reader operations are issued immediately in that first cycle. The operations for the other phases are decoded in parallel to the reader phase in the first cycle, and issued in the second.
In the second cycle, the main operations such as arithmetic and comparisons are issued.
At the end of the second cycle, two special phases run: function calls are dispatched sequentially and return, and then any pick operations run.
The final writer phase happens in the third cycle.
Operations that depend upon the output of other operations must wait for that operation to be completed. On conventional architectures this means that these operations must be in subsequent instructions and execute in subsequent cycles.
On the Mill, the results of a phase are available immediately to the operations in the next phase in the same cycle, and so dependent operations can be in the same instruction if those operations are in sequential phases.
The Mill can chain up to 6 dependent operations together and execute all of them in a single instruction.
This has advantages over a classic approach in tight loops, for example. The Mill is able to perform a strcpy loop as 27 operations in a single instruction, chained together through phasing.
[See talk: Execution]
Speculative Execution
The Mill can perform operations speculatively because operand elements have special meta-data and can be specially marked as invalid (Not a Result; NaR) or missing (None). Individual elements in vectors can be NaR or None.
The Mill can speculate through errors, as errors are propagated forward and only fault when realised by an operation with side effects e.g. a store or branch.
A load from inaccessible memory does not fault; it returns a NaR. If you load a vector and some of the elements are inaccessible, only those are marked as NaR.
NaRs and Nones flow through speculable operations where they are operands. If an operand element is NaR or None, the result is always NaR or None.
If you try and store a NaR, or store to a NaR address, or jump to a NaR address, then the CPU faults. NaRs contain a payload to enable a debugger to determine where the NaR was generated.
For example: a = b? *p: *q; The Mill is able to load both the values pointed at by p and q speculatively because any bad pointers will return NaR and will only fault if the comparison causes them to be stored to a.
Nones are available as a special constant, used by the compiler.
If you try and store a None, or store to a None address, or jump to None, the CPU does nothing.
For example: if(b) a = *p; The Mill can turn this into a = b? *p: None; which allows *p to be loaded speculatively and executes the store only if the condition is met.
Floating point exceptions are also stored in meta-data flags with belt elements. The exceptions (invalid, divide-by-zero, overflow, underflow and inexact) are ORed in operations, and the flags are applied to the global state flags only when values are realised.
There are operations to explicitly test for None, NaR and floating point exceptions.
Technically, None is a kind of NaR; there are several kinds of NaR and the kind is encoded in the value bits. A debugger can differentiate between memory protection errors and divide by zeros, for example, by looking at the kind bits. The remaining bits in the operand are filled with the low-order-bits of a hash identifying the operation which generated the NaR, so the debugger can usually determine this too even if the NaR has propagated a long way.
The None NaR has a higher precedence over all other kinds of NaR so if you perform arithmetic with NaR and None values the result is always None; None is used to discard and mask-out speculative execution.
[See talk: Metadata]
Vectorising while-loops
[See talk: Metadata]
The Mill can vectorise almost all loops, even if they are variable and conditional iteration and contain flow of control or calls. It can do this because it can mask-out elements in the vector that fall outside the iteration count. The Mill performs boolean masking of vector elements using pick and smear operations:
Pick
The pick operation is a hardware implementation of the ternary if: x = cond? a: b;
Pick is a special operation which takes 0 cycles because it executes at the cycle boundary.
Pick takes a condition operand which it interprets as boolean (all values with the low-order bit set are true) and two data operands to pick between, based on the boolean.
The operands can be vector or scalar. If the data operations are vector and the condition operand is vector, the pick performs a per-element pick.
Smear
The smear operation copies a vector of boolean, smearing the first true value it finds to all subsequent elements. For example, 0,1,0,1 smears to 0,1,1,1. (smear operates on vectors of boolean, rather than bits in a scalar.)
The smearx operation copies a vector of boolean, offset one element. The first element is always set to false, and the second result is an exit flag indicating if any true elements were encountered. For example, 0,1,0,1 becomes 0,0,1,1: 1 and 0,0,0,1 becomes 0,0,0,0: 1.
Strcpy example
Please do not use unsafe functions like C’s strcpy! However, it is an elegant illustration of loop vectorisation. while(*a++ = *b++) {} is straightforward to vectorise on the Mill:
a can be loaded as a vector and b can be stored as a vector. Any elements in a that the process does not have permission to access will be NaR, but this will only fault if we try and store them.
The a vector can be compared to 0; this results in a vector of boolean, which is then smearx’ed. This can then be picked with a vector of None into b. The smearx offsetting ensures that the trailing zero is copied from a to b. The second return from smearx, recording if any 0 was found in a, is used for a conditional branch to determine if another iteration of the vectorised loop is required.
The phasing of the strcpy operations allows all 27 operations to be executed in just one cycle, which moves a full maximum vector of bytes each cycle.
Remaining
The remaining operation is designed for count loops.
Given a scalar, the remaining operation produces a vector of boolean and an exit condition that can be used for picks.
Given an array, the remaining operation produces the offset of the first true element.
For example, strncpy is a straightforward extension of strcpy. It would take the n count argument and use the remaining operation to produce a boolean vector to act as a mask, which it then ORs with the strcpy’s result vector from comparing to 0.
Memory
[See talk: Memory]
The Mill has a 64-bit Single Address Space (SAS) architecture with position-independent code. The advantage of SAS is that address aliasing between processes cannot happen, which allows numerous context transitions to happen in the hardware with no OS intervention and still have fairly simple hardware.
On-CPU caches all use virtual addressing, and virtualisation to main memory pages is performed by a Translation Lookaside Buffer (TLB) between the lowest cache level and main memory. The TLB can divide up DRAM pages on a cache-line granularity. The allocation of virtual memory is done in hardware by the TLB using a free list, and only needs Operating System (OS) intervention if the free list is exhausted.
Memory accesses on the L1 are checked by a high-speed Protection Lookaside Buffer (PLB) which operates on logical address ranges. This is executed in parallel with loads, and masks out inaccessible bytes. The PLB can protect ranges down to byte granularity, although large ranges are more common and efficient.
Pointers
Data pointers can be a full 64-bits but can also be 32-bits using special segment registers, and can be relative. There are special segment registers for the stack, generic code, continuations and for thread-local storage (which also enables efficient green threading).
Code pointers are 32-bit using separate special segment registers, and are usually encoded relative to the EBB entry point, which can be efficiently packed in the instruction encoding.
64-bit pointers have 3 reserved high-order bits which can be used for marking by the application e.g. by garbage collectors. There are distinct operations for pointer manipulation e.g. the addp operation for adding offsets. These operations preserve the high bits and produce NaRs if these bits are overflowed into.
Loads
The Mill has an exposed pipeline architecture. The latency of all operations is fixed and known to the compiler; this includes the latency of loads, because the compiler schedules when it needs the value.
The load instruction specifies the number of future cycles when it will retire, and the hardware has until then to pull the value up through the cache hierarchy. The load latency of top-level data cache is just 3 cycles.
Loads are, in truth, variable latency but the scheduling of loads in the future hides this latency and stalls are uncommon.
An EBB will typically issue its load instructions as early as possible, set to retire close to their consumers, and perform meaningful computations in the intervening cycles.
A pickup load operation specifies a handle rather than a cycle to retire on. Code can use the pickup operation to retire the load at a later point. Pickup loads can be cancelled.
The Mill CPU has a fixed number of retire stations, and called code may evict a caller’s in-flight loads if there are no free retire stations. The caller’s loads are serialised to spill and re-issued when the call returns. Loads in-flight across expensive calls can therefore act as a pre-fetch, bringing values from main memory into cache while the expensive calls are executing, even if those calls evict the caller’s retire stations.
Aliasing
Mill load operations return the value of memory at their retire time (rather than at issue time) in order to allow loads to be issued before potentially aliasing stores, as long as their retire time remains after those stores.
When a store issues, it broadcasts the range it is storing to to all retire stations. If a store range intersects an in-flight load range, the station re-issues its load.
This makes the Mill immune to false aliasing, and as the store ranges are propagated to all cores on a chip, immune to false sharing too.
Scratch
There is a small amount of per-call-frame very fast memory called scratch that can be used to store long-lived values from the belt. This is where code can store values that would otherwise fall off the end of the belt.
Code can explicitly spill and fill to and from scratch, which takes just 3 cycles.
Scratch preserves floating point exception flags, NaR and None markers and other meta-data.
Functions must declare up-front how much scratch space they need for temporary storage, and this space is private to the call; functions cannot see the scratch used by other functions, and their scratch is lost when they return.
Stack
Stack is special address space that is private to the function that allocates it. It is allocated in fixed cache-line lengths using the stackf operation, and is implicitly initialized to zero. When the function returns, the stack is automatically discarded.
Implicit Zero and Backless Memory
Reads from uninitialised memory are automatically zeroed. This includes main memory, and the belt, stack and scratch.
Cache lines and stack lines contain a validity mask and uninitialized values are zeroed by a load.
Reads from memory that is not committed in the TLB returns zeros, without committing the RAM. RAM is only committed on-demand when cache-lines are evicted from the bottom of the cache hierarchy and written to main memory.
Code Blocks and Calls
Code is organised into Extended Basic Blocks (EBBs). Each EBB has exactly one entry point, but may have many exit points. Execution cannot fall off the end of an EBB – there is always terminating branch or return operation.
Execution can only jump – by branches within an EBB, or calls to an EBB – to the entry point.
The Mill has built-in – and therefore accelerated – calling support. There is a call operation, which takes just one cycle. Parameters to the call can be passed in copies of caller belt items (specifying items and their order on the callee’s new belt).
EBBs that are called are functions, and have their own private belt, stack and scratch. EBBs that are branched to inside a function share this belt and scratch.
A function can return multiple values back to the belt of the caller. The caller specifies how many belt items it is expecting to be returned; if this does not match the actual number returned, the thread faults.
Call and branch dispatch takes just one cycle. There is a predictor that is pre-fetching likely-to-be-executed blocks.
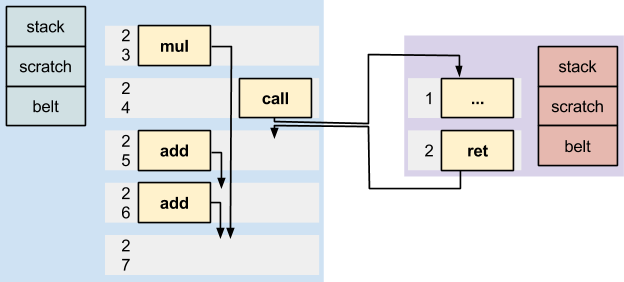
From the perspective of the caller, calls behave just like 1 cycle operations. If a caller has some other operations in flight during a call, these retire after the call has returned.
EBBs are a common organisation in compilers, and the Mill target is a near 1:1 translation of the compiler’s EBB and SSA internal representations.
[See talk: The Belt]
JonathanThompson
Participant
February 7, 2014 at 6:27 pm
Post count: 11
#609
This is one heck of a post. However, there appears to be a minor issue in one paragraph that needs to be fixed, though I’m not 100% of the details of how it should be fixed:
Under “Instructions and Pipelines” this appears wrong:
“Different pipelines have different mixes of FUs available, and the number of pipelines and their FU mix is Mill -model specific. There may be 4 or 8 integer pipelines and 2 or 4 floating point pipelines, for example. There are pipelines that handle flow control and pipelines that handle load and saves. In a mid-range Mill “Gold” CPU there are 33 pipelines of which 8 are integer and 2 are floating-point; the Mill Gold CPU can issue 33 operations per cycle, sustained:”
Unless I’m mistaken, the Gold isn’t mid-range: this is the most detailed information that’s been specified about the pipelines, so I can’t state how correct that is.
If there are other mistakes in all of this, I’m not able to spot it with the information I feel I have/understand. All considering, that’s a minor issue 🙂
- Art
  Participant
  February 7, 2014 at 7:07 pm
  Post count: 11
  #610
  Yes, Gold is a high end Mill member.
  Here is a more thorough enumeration of Gold’s 33 pipelines:
  8 pipes that do single output “reader” operations
  4 pipes that can do either integer (including multiply) or binary floating point (also including multiply) operations
  4 pipes that can only do integer (not including multiply) operations
  4 pipes that can do either immediate constant, load/store or control transfer (branch, call) operations
  4 pipes that can do either immediate constant or load/store operations
  4 pipes that can do pick operations
  5 pipes that can do “writer” operations
  There is a bit more to it than that, but those are the major units of interest.
- Will_Edwards
  Moderator
  February 7, 2014 at 11:50 pm
  Post count: 98
  #611
  Sorry, I could have been over-enthusiastic. I can imagine a Mill with more L2 and L3, wider belt, more FP, higher clock rate and so on 🙂
  But yes, the Mill is high end compared to today’s CPU cores, perhaps? 😉
  I will fix the post when I am next on a laptop.
  This reply was modified 10 years, 10 months ago by Art. Reason: correct formatting to intended
  - JonathanThompson
    Participant
    February 8, 2014 at 12:02 am
    Post count: 11
    #613
    You’re human (darn it, right?).
    I’m wondering what the practical differences would be with the Platinum Mill: the one with 64 belt positions.
    However, I realize that the cycle limit time for the double crossbar for the belt would definitely lengthen the instruction cycle, OR would require more clock cycles to account for that difference, which would likely make the circuitry not merely twice as much (it wouldn’t be anyway due to the double crossbar) but scale a little closer to squared. Meanwhile, in most cases, I’m not sure how much more parallelism you could extract, and what the cost would be in power for typical workloads.
    That’s one major thing I see with Intel with the x86 (32 and 64 bit) architectures: while the process size goes down, it’s easy for them to add more cores on the same area, but most practical workloads (non-server) typically rarely use more than 2 threads: I believe this is a huge reason Apple has gone the direction they have, with 2 higher performance cores in their ARM devices, with one core more likely used for all GUI stuff, and the other core for the background I/O and computations. Besides the parallelism of 2 threads being an easy reach for typical applications (general purpose GUI apps with I/O and background computations) there’s also the memory bandwidth to consider: if a modern superscalar OOO core is waiting 1/3 of its instruction cycles for main memory, adding more cores just means that more cores are idling, waiting for memory to have anything to compute.
    Unless I’m mistaken about the nature of the beast, memory I/O also has additional power requirements for storing/retrieving data above regular refresh power, and actively used, RAM and the associated circuitry is one of the more major power consumers: thus, reducing memory I/O for a given amount of useful computation is also a power usage reduction.
    This reply was modified 10 years, 10 months ago by JonathanThompson.
    - Will_Edwards
      Moderator
      February 8, 2014 at 2:28 am
      Post count: 98
      #615
      I was careful to say wider belt, meaning more elements in a vector, rather than longer belt because I imagine its diminishing returns and stresses instruction cache and so on.
      The key thing is that it is straightforward to simulate variations and evaluate them on representative target code. I’m sure that the current configurations haven’t been plucked from thin air, but rather represent what is considered the most advantageous mix for the first cut.
      I do want a Platinum Mill on my desktop and to hell with cooling! When we have a monster for gaming rigs, compiler rigs and for the fun of it, then we can dream of an Unobtainium Mill.
      - Ivan Godard
        Keymaster
        February 8, 2014 at 3:18 am
        Post count: 689
        #617
        Unobtainium yet? Coming right up.
        Note on terminology: we refer to the MIMD dimension as the width of the machine, and the vector size as the height. Width is thus an encoding matter, which is related to but not the same as the number of Belt positions, which we call the length.
    - Ivan Godard
      Keymaster
      February 8, 2014 at 3:14 am
      Post count: 689
      #616
      Recall that there are two dimensions of parallelism on a Mill: MIMD width (number of slots, == number of concurrent operations), and vector height (in bytes). It’s hard to find a code that can use more than a Silver in open code; there’s just not that much ILP in the code, even with phasing. In pipelined loops there’s all the ILP you want, but once you have every op in the loop running pipelined then all you can do is unroll and do several iterations at once. Even HPC loops are usually only one or two instructions on a Gold, so it’s not clear that there is much use for greater width. While wider is certainly possible, we spec’d Gold to be at what we expected to be the point of diminishing returns for width.
      However, even on a narrower configuration there is some use for higher, i.e. more SIMD even if not so much MIMD. Those pipelined loops can often be vectorized, and if the iteration count is big enough to use the height then that’s probably the best way to get raw horsepower.
      Of course, all the horsepower in the world will bot give you anything if you are memory bandwidth limited, and, as you suggest, bandwidth is likely to be the practical limit.
      - CarVac
        Participant
        February 8, 2014 at 8:09 am
        Post count: 4
        #619
        What can you change in CPU design to reduce memory bandwidth issues? Would you be able to, say, have 4 or 6 memory channels instead of the 2 typical today?
        Given the memory bandwidth limitations and the fact that Mill can pipeline AND vectorize loops, wouldn’t trading a bit of latency help throughput on these very short loops?
Ivan Godard
Keymaster
February 8, 2014 at 11:13 am
Post count: 689
#622
Yes, you can have a wider path to DRAM, although there are board-level hardware issues; the costs and benefits are independent of the ISA. And you can reduce the DRAM latency by stacking and similar approaches; this to is independent of ISA.
Where the ISA can help is twofold: reducing the total DRAM traffic; and changing the timing. The Memory talk showed ways that the Mill cuts the traffic bandwidth; not a lot (perhaps 25%), but every bit helps. And the Mill has ways to alter the timing, but the patents aren’t in on those yet.
As for trading, there not much left to trade. On many conventionals there are serious overheads setting the machine up for vectors, but the Mill doesn’t have that problem (and there’s no fundamental reason others should either). You might as well vectorize a short loop on a Mill; even if it turns out that there’s only one element in the array, the cost of a vector and a scalar code will be very close, and vector wins big once the element count exceeds the vector height. The only real advantage of a scalar loop for very short arrays is in power usage – they are equally fast, but dealing with the Nones in the unused elements does cost power.
Not sure I’ve answered your question; feel free to try again.
squizzle
Participant
March 27, 2014 at 1:56 am
Post count: 5
#834
Could you expand upon what the cycles / phasing looks like with multi-cycle ops such as a multiply?
- Will_Edwards
  Moderator
  March 27, 2014 at 2:53 am
  Post count: 98
  #835
  The multiply op belongs in the execute phase, so issues in the second cycle of the instruction.
  The number of cycles it takes is member dependent, and operand width dependent, and dependent on the type of multiply (integer, fixed point, floating point, etc). Multiplying bytes is quicker than multiplying longs, and so on. But the specializer knows the latencies and schedules appropriately.
  Lets imagine it takes 3 cycles, which includes the issue cycle. The instruction issues on cycle N, but the multiply operation issues on cycle N+1 and retires – puts the results on the belt – before cycle N+4.
  The CPU likely has many pipelines that can do multiplication, as its a common enough thing to want to do. The Gold, for example, has eight pipelines that can do integer multiplication and four that can do floating point (four of the integer pipelines are the same pipelines as the four that can do floating point).
  So on the Gold, you can have eight multiply ops in the same instruction, and they all execute in parallel. Furthermore, even if a pipeline is still executing an op issued on a previous cycle, it can be issued an op on this cycle. And each multiply can be SIMD, meaning that taken altogether the Mill is massively MIMD and you can be multiplying together a staggeringly large number of values at any one time, if that’s what your problem needs.
cheery
Participant
March 29, 2014 at 12:40 pm
Post count: 7
#877
I just read this post and watched few videos again.
The execution and load format are different in this architecture. Whenever a program wants to run something, it will push it to the specializer, which translates a load format into execution format that fits this machine.
So the load formatted code doesn’t contain details about the belt size or operation latencies. Which properties does the loadcode preserve compared to the execode?
How fast is the specializer in theory? It needs to schedule a graph of operations into shortest possible instruction sequence that can be executed by the machine, because every instruction counts unlike in OOE -machines. Each operation in the graph has a duration it takes and dependencies to other operations. There are logical end-points – the data stores and control flow branches. It sounds like the specializer needs to compute the critical path from the code, which is longest path problem and that can be computed in linear time. I’m just not sure what else it’d need to do, I’ve only thought about it for three days, not sure about what I’m looking at.
It also looks like the loops need to be vectorized by the compiler. Is it a hard thing to do? Sounds like something easy for tracing JIT compiler, hard for a traditional compiler.
If these are topics of the upcoming video lectures, I can wait for the videos. It’ll be interesting to follow it all. It may very well become an exciting new platform.
- This reply was modified 10 years, 8 months ago by cheery.
- Ivan Godard
  Keymaster
  March 29, 2014 at 4:01 pm
  Post count: 689
  #889
  The load format knows that it is a Mill and has done operation selection under the assumption that the full abstract Mill operation set is available. The specializer replaces missing ops with emulation subgraphs, often calls but sometimes in-line, that do the same job. The canonical example is floating point, which some Mill family members lack completely.
  The load format also knows the widths of each operation. Even though width is not in in the final encoding (it’s represented in the metadata), the compiler that generates load format knows the widths of the arguments, so load format distinguishes add-byte from add-half, and so on. The specializer also substitutes emulation for missing widths, notably on members that lack hardware quad precision.
  Load format itself is a serialized forest of data- and control-flow graphs. Emulation substitution is O(N) in program size, and is done on the fly as the graphs are de-serialized.
  The major task of the specializer, and the time critical one, is operation and instruction scheduling. We use the classic VLIW time-reversed deterministic scheduler, which is O(N) for feasible schedules. Not all schedules are feasible because we can run out of belt and must spill to scratchpad. In such a case, the specializer modifies the graph by inserting spill-fill ops and reschedules, repeating if necessary. A feasible schedule is guaranteed eventually, because the algorithm reduces to sequential code which is feasible by hardware definition. The time depends on the number of iterations before feasibility, which is at most N giving an O(N^2) worst case. However, studies show O(N^1.1) is typical, i.e. few EBBs need spill, and more than one iteration is essentially never seen.
  That’s a big-O analysis, and the constants matter too in the actual speed of the specializer. However, the constants depend on the horsepower of the Mill doing the specialization, and we don’t have sims yet for anything that complex. We don’t expect speed to be an issue though; disk latency is more likely to dominate.
  There are a few cases in which best member-dependent code is not just a matter of schedule. An example is the decision of whether a given short-count loop is worth vectorizing, which decision depends on the vector size of the member. The compiler normally does the vectorization, and the only part the specializer plays is to supply a few constants, such as the amount to advance addresses by with each iteration. However, in some cases it is better not to vectorize at all, and the vector and scalar loops are quite different.
  In such cases the load format gives alternate code choices and a predicate that the specializer evaluates. The chosen code is then integrated with the rest of the program in the same way that emulation substitution is done. We want to compiler to be sparing in its use of this facility though, to keep the load-format file from blowing up too big.
  I expect that there will be a Specializer talk, but not until the new LLVM-based compiler is at least up enough for public view.
lookaside
Participant
November 10, 2014 at 4:00 pm
Post count: 4
#1519
I was attempting to write a few programs using this model but I ran into a problem I couldn’t solve. I might be overlooking something but I found that if you have an instruction that conditionally pushes something onto the belt, you can no longer know the indices of the other belt positions. For example…
If you had this code:
add b0, b1
if(cond) {b0++}
And you wanted to read the result from the addition, how do you know whether to read it from b0 or b1? I’m thinking you’d have to restore the result if the condition is true but that could potentially double code size…
Hopefully there’s a simple solution.
- Veedrac
  Participant
  November 10, 2014 at 8:07 pm
  Post count: 25
  #1520
  I imagine you would do something like
  add b0, b1 pick cond, b0, None add b0, 1
  “None” effectively absorbs all computation without error. So you would have:
  [12, 11, cond=1, ...] [23, 12, 11, cond=1, ...] (add b0, b1) [23, 23, 12, 11, cond=1, ...] (pick cond, b0, None) [24, 23, 23, 12, 11, cond=1, ...] (add b0, 1)
  or
  [12, 11, cond=0, ...] [23, 12, 11, cond=0, ...] (add b0, b1) [None, 23, 12, 11, cond=0, ...] (pick cond, b0, None) [None, None, 23, 12, 11, cond=0, ...] (add b0, 1)
  It’s not obvious how to turn None into its value, though. You could do
  add b0, b1 # store pick cond, b0, None add b0, 1 # store (may do nothing) # load
  but that seems like a lot of overhead to do very little.
  —
  Obviously, though, in this case the best option is just
  add b0, b1 add b0, cond
  🙂
  This reply was modified 10 years, 1 month ago by Veedrac.
  This reply was modified 10 years, 1 month ago by Veedrac.
  This reply was modified 10 years, 1 month ago by Veedrac.
  - lookaside
    Participant
    November 11, 2014 at 6:07 am
    Post count: 4
    #1525
    Missed the reply button. Responded to you below.
- Ivan Godard
  Keymaster
  November 17, 2014 at 10:16 am
  Post count: 689
  #1538
  Control-flow join points must normalize the belt so that each live operand is in the same place regardless of how the join was reached. The best normalization code depends on the number of live values and their respective positions.
  The completely general solution is to choose the belt layout of one inbound path as canonical, and add a conform operation to each other path to force the belt on that path to match (conform with) the canonical. If you have profile info then the canonical path should be the one most commonly taken.
  If the values to be normalized are in the same relative order on all paths (although not the same actual positions) then putting a rescue operation on each path gives a cheaper encoding than conform.
  If the code between the dominator and the join on each path is speculable (as in your example) then if-conversion will give by far the best code, replacing the branch with one or more pick operations. In modern fabrication processes it cost little more to do a wasted arithmetic operation than to leave the functional unit idle for that cycle. However, if there is more code than available FU cycles this speculation strategy will increase latency, so using pick is most advantageous on wide family members. However, overall program performance may still be better with pick if the branch does not have consistently predictable behavior; the speculation latency of the pick will be exceeded by the mispredict penalties of the branch.
  Lastly, in some cases (including your example) it is possible to do a poor-man’s conform using a null arithmetic operation, typically ORing with an immediate zero. Then if the code takes the true path there will be a result dropped by the add, and if it takes the false path then a copy of the value will be dropped by the OR, and in either case the correct value will be at the front of the belt for further processing.
  The specializer algorithm currently if-converts everything if the operations are speculable, and it inserts conform ops if not. A later peep-hole step then changes the conforms to rescues if that is possible.
lookaside
Participant
November 11, 2014 at 5:13 am
Post count: 4
#1524
Yeah I had that solution too for cases as simple as my example. The problem is when you try to scale that to a larger conditional code block that could push several arguments on the belt. Another example:
```
add b0, b1
if(cond) {
mult b0, b1
div  b0, b1
add  b0, b1
sub  b0, b1
xor  b0, b1
and  b0, b1
}
```
That would either be turned into a branch or you could make each statement conditional with pick but that would increase code size, execution time, and could push a lot of useless stuff onto the belt just to keep indices consistent. Only other option I see would be to store anything important / send it to the spiller and restore them after the branch was executed but that’s still slow because latencies. 🙁
Will_Edwards
Moderator
November 11, 2014 at 7:17 am
Post count: 98
#1526
You’re both quite right!
When there’s an if(/else) the compiler/specializer can encode it as branches or inline it using if-conversion, and can evaluate which is best (which may differ on different Mill members).
The if(/else) can be solved by the if and the else blocks being their own EBBs with a conditional branch, or by computing both the if and the else blocks in parallel.
As the Mill is such a wide target (especially on the middle and high end Mills) with so many pipelines and because loads can be hoisted up to their address being computable without fear of aliasing its often so that many if(/else) can be done in parallel speculatively and this is a huge win for performance. Usually you only have to introduce some strategic Nones or 0s to nullify some untaken paths you are executing speculatively rather than needing lots of conditional ops and picks.
Its hard to get a feel for this without concrete code and we will be making a real simulator available in the new year.
One note, its important that the belt be consistent at all times but its irrelevant what the belt contents are if they are unused. If all instructions after a certain point are consuming slots 0 and 3 then it doesn’t matter the values of any other belt slots. There are cheap fast opcodes for moving items to the front of the belt like rescue and conform to do this rearrangement.
lookaside
Participant
November 11, 2014 at 3:35 pm
Post count: 4
#1530
That seems inefficient compared to a conventional register system. On the Mill, if my example code were implemented with pick, the code would be twice the size and always execute whether the condition was true or false (all for keeping track of previous arguments). A register system would just branch and execute the code or not. The mill makes up for this with parallelization but if a register system were equally parallel, it seems it would have better performance no?
- Will_Edwards
  Moderator
  November 13, 2014 at 10:57 pm
  Post count: 98
  #1531
  From looking at raw assembly code for a conventional processor you get the impression that things happen linearly and, as you say, “a register system would just branch and execute the code or not”. But looking at the code is thinking about the ‘programming model’, and is not actually how things execute under the hood so to speak.
  And unfortunately there are catches; things don’t happen linearly (modern fast CPUs are “Out-of-Order”) and branches aren’t just to be taken cheaply. Branching – or rather, mispredicting a branch – is shockingly expensive, and OoO compounds that.
  Modern CPUs have all introduced new op-codes to do “if-conversion”, although with mixed success. cmov and kin are the new darling opcodes.
  The Metadata talk describes speculation and is warmly recommended.
- Will_Edwards
  Moderator
  November 16, 2014 at 9:54 am
  Post count: 98
  #1537
  There are many types of “efficiency” and you got me thinking about power economy, which is a very important aspect to all this:
  There is the opportunity for multi-cycle instructions to fast-path NaRs, and I’m particularly thinking about monsters like multiply… whereas a real multiply takes a lot of power especially for large operand widths and vectors, a NaR can cause a cheap short cicuit so you can make substantial gains in power efficiency with speculation verses the hardware needed to do prediction.
  - Ivan Godard
    Keymaster
    November 17, 2014 at 10:23 am
    Post count: 689
    #1539
    Whether power-shorting on NaR (and None) arguments pays depends on how common they are and whether the case can be detected early enough to take effect – it can take more than a cycle for a signal to cross a multiplier! Power shorting might pay on a native divide, but a multiplier would likely have already committed the power before it could figure out that it didn’t need to do so. And of course we don’t expect to be implementing native divide.
    - Will_Edwards
      Moderator
      November 18, 2014 at 8:45 am
      Post count: 98
      #1543
      We’re both right 🙂
      The hardware gang are hopeful that we can have NaR low-power paths for things like multiply.
LarryP
Participant
November 17, 2014 at 3:14 pm
Post count: 78
#1540
In order to propagate NaRs and Nones properly, I think all ALUish operations (including mult) will have to check their inputs explicitly for NaRs and Nones. Which leads to a question: What is the proper result for NaR * None?
Which leads to another puzzler: What should be the behavior when a None gets involved in an address calculation? And what is the Mill’s behavior when such an effective address is used by a load or a store operation?
- Symmetry
  Participant
  November 17, 2014 at 4:31 pm
  Post count: 28
  #1541
  A None plus a NaR makes a None. Think of it as combining a “discard this” and a “causes problems if this isn’t discarded”.
  If you’re using an None to calculate a load the load is skipped and you get another None on the belt. If you’re storing a None that’s a no-op.
  But come to think of it, I’m not sure what happens when you use a NaR to do a load. Does it cause a fault immediately, or does it just drop a NaR on the belt?
  - Veedrac
    Participant
    November 17, 2014 at 6:36 pm
    Post count: 25
    #1542
    By far the most of the operations in the Mill instruction set can be speculated. What this means is, if an operand to the operation is None or Nar, all the operation does is to make the result None or NaR, or combine the status flags in the case of floating point operations in the result. This is even true for the load operation.
    From http://millcomputing.com/wiki/Speculation#None_and_NaR
LarryP
Participant
December 30, 2014 at 5:26 am
Post count: 78
#1604
Greetings all,
It turns out that Ivan has answered (in the metadata thread) regarding the result from a NaR and a None in a normal (read two-input, exu-side) operation: The None wins; see his response #558:
http://millcomputing.com/topic/metadata/#post-558
IMHO, this still leaves unclear what happens when either a None or a NaR are inputs to an address calculation (e.g., as base, offset or index inputs the the address calc.), either as a separate calc or as part of a load or store operation. The rules for address calculations (on the flow side) might be different than for exu-side ops.
We know that Nones as data values silently act as no-ops when stored, and that inaccessible addresses return Nones when loaded from. However, I’m still puzzled re what load/store ops do when their effective address is None. My best guess is that a NaR effective address will make both loads and stores fault, but the desired behavior may well be different for an effective address of None.
- This reply was modified 9 years, 11 months ago by LarryP.
- Ivan Godard
  Keymaster
  December 30, 2014 at 2:59 pm
  Post count: 689
  #1608
  You ask good questions 🙂 (A variation on the Chinese curse: “May you receive good questions”). I had to go look at the code in the sim to answer.
  We detect various problems in the load/store logic in different ways and at different places, so please bear with a rather complex explanation.
  The generic Mill address is base+(scaled index)+offset. Offset is a literal in the instruction; index if present is from the belt, and base may be either from the belt or one of a specific set of specRegs.
  SpecRegs cannot be None or NaR. However, the encoding used for the specReg (in the instruction forms that use it) may have bit combinations that are not valid. Use of such a combination, as with other illegal encodings, reflects a compiler bug and gets a fault and the usual trip through handlers. There is special handling for tpReg (“this” pointer). If tpReg is used as a base when the register has not been set then a NaR is passed to the rest of the address calculation.
  There are a different set of checks when the base is a pointer from the belt. There is a width check that the argument is a scalar of pointer width; failure faults because this is a compiler bug. None/NaR is passed on to the index check.
  If the index is present there is a width check and we fault a vector index; a scalar index can be of any width. The index is then resized to pointer size, and scaled. If the resize or scaling overflows then we fault. This should probably pass on a NaR instead, but does not in the present sim. If the index was a None/NaR then these are passed on. For a missing index we pass on a zero.
  At this point we have a base, index, and offset input to the 3-input address adder, and either base or index could be None/NaR. The address adder applies Mill pointer arithmetic rules, and in particular checks for overflow into the non-address bits in the pointer. An overflow is noted.
  Now comes the None/NaR handling: if either of the base or index were None then the final address is one of the input Nones, otherwise if either of the inputs is NaR or the address-adder result overflowed then the final address is one of the NaRs from the input or a ne NaR if only overflow happened. Otherwise the final address is normal.
  Now, if the operation is a store and either the final address or the value to be stored is None then the store is suppressed. If either the final address or the value to be stored is NaR then we fault. Otherwise the store proceeds, but may fault the protection check on the final address.
  If the operation is a LEA and the final address is None then the result is the None as a pointer-sized scalar. Otherwise if the final address was NaR then the result is the NaR as a pointer-sized scalar. Otherwise the result is the final address as a pointer-sized normal scalar.
  If the operation was a load and the final address was None then the result is an operand of the loaded scalarity and width all of whose elements are the None scaled to the element width. Otherwise if the final address was NaR then the result is an operand of the loaded scalarity and width all of whose elements are the NaR scaled to the element width. Otherwise the final address is normal and the loads proceeds.
  You’re welcome.
LarryP
Participant
December 31, 2014 at 8:42 am
Post count: 78
#1609
Ivan,
Sorry my question took so much time/effort to answer. That said, I’m very pleased to gain a little glimpse into your simulator, just as I am to see that this issue had already been thought through in considerable detail. Deferring faults as far as feasible seems like a win for speculation.
One rare downside I see is that a byte vector loaded from a NaR address will contain such short NaRs that the hash in the payload may not be much help for tracking down the source of the resulting NaRs. And since the silent behavior of Nones may be nonintuitive to people (esp. those porting existing code to the Mill), some Mill-specific compiler switches (e.g. for extra tests and warnings for Nones/NaRs as addresses) may be desirable — after LLVM is generating usable Mill code.
Happy new year to you and the whole Millcomputing team,
Larry
- This reply was modified 9 years, 11 months ago by LarryP.
David McCammond-Watts
Participant
January 2, 2015 at 8:55 am
Post count: 13
#1611
Not that it matters terribly much (not interested in a religious war over it) but I’m curious if the Mill is planned to be little endian or big endian?
LarryP
Participant
January 2, 2015 at 9:02 am
Post count: 78
#1612
David,
Endianness: Internally little-endian, your choice for memory.
From one of Ivan’s posts http://millcomputing.com/topic/metadata/#post-318
Author
Posts